ITIS

 Leonardo da Vinci ■ Lanciano

LSTS

    La forza di Casimir.

(Credit & Copyright: Federico Capasso, Lucent Technologies).

      La fisica quantistica è stata sicuramente, insieme alla teoria della relatività, la rivoluzione più importante della fisica del XX secolo. Nonostante i suoi principi vadano molto spesso contro il nostro senso comune o la logica della fisica classica, le dimostrazioni sperimentali della sua validità sono ormai talmente tante da non metterla più in discussione, almeno nelle linee essenziali. Tra gli ultimi effetti rivelati e misurati, derivati dalla fisica quantistica, c’è l’effetto Casimir, una forza di attrazione tra due lamine metalliche, elettricamente neutre, poste a distanza molto ravvicinata; una forza originata letteralmente dal nulla, non dovuta né alle forze elettromagnetiche, né alle forze gravitazionali.

     Per spiegarlo dobbiamo prima porci una domanda all’apparenza semplice: il “vuoto” è realmente vuoto? La fisica classica definisce il “vuoto” come “Assenza di materia o energia in un volume di spazio”. Per Democrito il vuoto era “lo spazio entro cui si esercita il movimento”. Concezione avversata dagli Aristotelici che, partendo dal meccanismo del moto, dovuto all’azione dell’aria che si precipita ad occupare lo spazio vuoto lasciato dall’oggetto in movimento, arrivarono a sostenere che il vuoto non poteva esistere in natura, ipotizzando quell’”horror vacui”, che avrebbe perseguitato i fisici fino all’esperimento di Torricelli. Se il concetto di vuoto era soggetto a diverse spiegazioni e definizioni, era chiara invece nell’uomo comune, l’idea che nel vuoto non esistesse nulla, proprio per la sua definizione.

    La fisica quantistica ci costringe, ancora una volta, ad abbandonare questa idea , presentandoci un vuoto che è un continuo ribollire di particelle, in virtù del principio di indeterminazione di Heisenberg. Tale principio, sfruttato tra l’altro in tutti i laboratori del mondo per generare particelle, si presenta, nella forma di nostro interesse, come:

DE * Dt  ≥  h/2p = ħ

dove h è la costante di Planck ( 6,626 10 ^-34 Joule*secondo ) e ħ la costante tagliata, come comunemente viene indicata.

     Il principio di Heisenberg afferma, tra l’altro, che possono esistere delle particelle di qualunque energia DE per un tempo Dt, però, brevissimo, tale da non violare la relazione scritta; tali particelle spariranno quasi immediatamente a meno che non si compensi la natura con una quantità di energia corrispondente, come si fa quando si generano particelle elementari negli acceleratori. Nel vuoto quindi c’è una continua creazione-distruzione di particelle virtuali che sono nello stesso tempo, sempre secondo la fisica quantistica, particelle e onde, la cui lunghezza d’onda l dipende dall’energia E secondo la relazione (m è la massa della particella, v la sua velocità e h la costante di Planck)

l =  h / (mv) = h  /  

       E qui arriviamo finalmente al misterioso effetto Casimir, previsto teoricamente da Hendrick Casimir , un fisico olandese, già nel lontano 1948, ma misurato sperimentalmente solo nel 1996.

      La fisica delle onde, con i principi di sovrapposizione ed interferenza, ha in sè la conseguenza che in determinate condizioni , possono esistere solo onde con una lunghezza d’onda particolare.

Chi ha dimestichezza con la chitarra, o con altri strumenti a corda, sa che i modi di vibrazione di una corda con estremi fissi a distanza L tra loro, sono solo quelli illustrati in figura, per i quali si ha che la lunghezza d’onda l deve soddisfare la relazione L = n (l/2), con n intero qualunque (onde stazionarie).

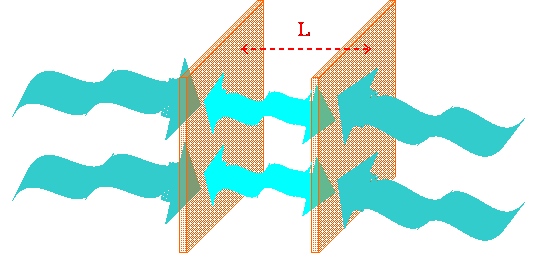
       Fenomeno analogo succede se abbiamo delle onde, ad esempio delle onde luminose, all’interno di una cavità, limitata da superfici riflettenti. Supponiamo ora di avere due lamine metalliche di superficie A leggermente distanziate di una distanza L fra loro (figura seguente): anche in questo caso, se ci limitiamo a considerare la direzione perpendicolare alle superfici, all’interno sarà possibile l’esistenza solo di quelle particelle, con lunghezza d’onda l, che soddisfano la relazione   L = n (l/2) con n numero intero qualunque.

      Possiamo allora distinguere, nel disegno, uno spazio “vuoto” tra le lamine in cui possono crearsi solo particelle virtuali con determinate lunghezze d’onda, tali cioè da soddisfare la relazione scritta, mentre fuori c’è uno spazio “vuoto” dove è possibile che si creino particelle con lunghezza d’onda qualsiasi. Quando una particella virtuale nella sua effimera esistenza, prima di scomparire di nuovo, urta contro una delle lamine, determina su di essa una certa forza per unità di tempo, e quindi una certa pressione, secondo i principi di conservazione dell’impulso. Questo modello è lo stesso usato per studiare la pressione di un gas all’interno di un recipiente chiuso, secondo le leggi classiche della termodinamica.

    L’azione complessiva sulle lamine sarà la somma di tutte le possibili azioni delle singole particelle virtuali. Per lo spazio esterno alle lamine questo comporta dover fare l’integrale di tutti i possibili contributi delle particelle virtuali che vi si creano, con tutte le lunghezze d’onda possibili, che saranno infinite. Per le particelle che si creano all’interno, invece, poiché sono possibili solo determinate lunghezze d’onda, dovremo fare una sommatoria dei contributi, anch’essa infinita. E’ evidente che all’esterno avrò un numero di particelle virtuali possibili, più numeroso che all’interno, anche se entrambi di numero infinito. E qui interviene la potenza dell’analisi matematica, che afferma che la somma di infiniti termini infinitesimali può essere una quantità finita e, in particolare nel nostro caso, la differenza fra l’integrale sui contributi esterni e la sommatoria dei contributi interni è finita e positiva, determinando una forza che tende ad avvicinare le due lamine tra loro.      

      L’espressione di questa forza ricavata analiticamente è:

     In essa h è la costante di Planck, c la velocità della luce, A l’area delle lamine e L la loro distanza. Il valore di tale forza F, per due lamine di superficie pari a 1 cm² poste a distanza L = 1 mm, è di 1,29*10 ^-19 Newton. Un valore estremamente piccolo che fa capire come mai la sua verifica sperimentale sia stata possibile solo nel 1996, e in particolare nel 1997 da Lamoreaux con un sofisticato apparato sperimentale. Oggi, però, che con le nanotecnologie stiamo arrivando a distanze in cui l’effetto Casimir non è trascurabile; si sta pensando di sfruttarlo  nella realizzazione di nano-sensori di distanza. (Vedere l’articolo sui Mems già pubblicato su “IL Leonardo”, e l’immagine di apertura).

(Credit & Copyright: Federico Capasso, Lucent Technologies)

    Nella figura b sopra riportata, si può vedere la realizzazione, con tecniche di micro-ingegneria, di una piastra di silicio policristallino, sospesa, in grado di ruotare quando viene avvicinata una pallina metallizzata ad una delle sue estremità; nella figura c è evidenziata, ancora più ingrandita, una delle barrette di torsione che tengono la piastra, mentre nella figura a è illustrato il meccanismo di funzionamento di tale sistema. (Viene anche mostrato l’apparato sperimentale)

     La scienza sta insomma scoprendo una nuova tecnologia; si passa, infatti, dall’ingegneria dei materiali ad una ingegneria del vuoto. Piuttosto affascinante, non credete?

Domenico Di Bucchianico

Back