|
ITIS |
IstitutoTecnico
■
LiceoTecnologico Leonardo da Vinci ■ Lanciano |
 |
LSTS |
 L'angolo della scienza
L'angolo della scienza |
|||
|
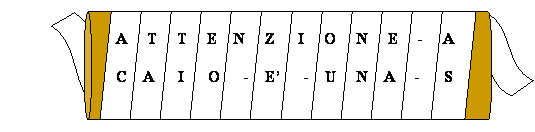
Crittografia e matematica. Fin dalla nascita delle prime comunità umane, spesso in conflitto fra di loro, sorse il problema di riuscire a comunicare a distanza, senza che i messaggi potessero esser intercettati da eventuali nemici. Nelle “Storie” di Erodoto si narra della guerra di Serse, re dei persiani, contro la Grecia. Un certo Demarato, venuto a sapere dell’imminente attacco contro Sparta, cercò di avvertire i suoi abitanti senza che i persiani se ne accorgessero. Asportò la cera da una delle tavolette usate per la scrittura ed incise il messaggio segreto direttamente sul legno del fondo; ricoprì poi con nuova cera e lo mandò tramite un messaggero a Sparta. La moglie di Leonida, quando il messaggio giunse a destinazione, intuì che dovesse recare un messaggio segreto e trovarono quindi l’incisione sul legno. Quel provvidenziale messaggio permise agli Spartani di battere Serse nel 480 a.c., cambiando forse il corso della storia. Altro stratagemma utilizzò un tale Istieo, nell’antica Grecia, che voleva comunicare ad Aristagora di ribellarsi ai dominatori di allora, senza che questi lo venissero a sapere. Fece rasare la testa ad un servo e sulla testa fece scrivere il messaggio. Quando i capelli ricrebbero il servo fu spedito a Mileto. Esistevano addirittura dei trattati militari come quello di Enea Attico ed il libro degli “Stratagemmi” di Frontino in cui si insegnava a nascondere i messaggi tra i due strati della suola di una scarpa, cuciti all’interno di un otre, scritti sulle foglie con cui venivano tamponate le ferite, oppure occultati in piccoli pezzetti di piombo indossati da una donna come orecchini o cuciti sotto le falde di una corazza. Questi esempi da un lato mostrano la necessità della comunicazione segreta, dall’altro la scarsa sicurezza offerta da tali sistemi: una revisione accurata del messaggero bastava a scoprire il messaggio segreto. La tecnica dell’occultamento dei messaggi viene oggi indicata come “steganografia”, particolarmente usata ai nostri giorni, vista la diffusione dei computer. E’ molto facile con semplici programmi occultare messaggi segreti in file immagine e file sonori, senza che l’eventuale osservatore o ascoltatore se ne accorga. Nelle figure che seguono potete confrontare due immagini apparentemente uguali, solo che in una di esse (l’immagine a destra) è celato un messaggio. E’ impossibile accorgersene a prima vista, a meno che non si sappia già che l’immagine nasconde qualcosa e quindi utilizzare un semplice programmino di estrazione dell’informazione, a patto però, di conoscere la password utilizzata per la codifica da chi trasmette. Ma non è questo l’argomento che voglio ora affrontare. copyright Marcello Guidotti, 1999 (http://www.nemesi.net/stegano.htm) La tecnica alternativa alla “Steganografia” è quella della “Crittografia”, dal greco Kryptòs che significa nascosto. In essa non si cerca di nascondere un messaggio ma il suo significato. Si modifica il testo da trasmettere usando un codice concordato che solo mittente e destinatario conoscono e poi si invia tranquillamente. Chi lo dovesse intercettare non potrebbe decodificarlo, a meno di conoscere la chiave di scrittura; potrebbe solo distruggerlo per impedirgli di arrivare a destinazione. Di una tecnica di crittografia rudimentale, ma efficace, ci parla addirittura Plutarco illustrando il funzionamento della “Scitala” usata dagli spartani. Si tratta di un cilindro di legno di diametro prefissato attorno al quale viene avvolta a spirale una striscia di cuoio, di papiro o altro su cui scrivere. Quando la striscia, su cui veniva scritto il messaggio per la lunghezza del cilindro, veniva srotolata apparivano solo una serie di lettere senza significato. La decodifica avveniva semplicemente riavvolgendo la striscia su di un cilindro dello stesso diametro di quello iniziale. Uno dei più famosi sistemi di crittografia dell’antichità, ripreso dall’abate Tritemio nel XV secolo nel suo trattato sulla “Steganographia” nel quale illustrava anche diversi sistemi di crittografia misti a sistemi di steganografia, fu quello attribuito a Cesare. Nel “De bello gallico” viene illustrata la tecnica utilizzata per comunicare segretamente con Cicerone , assediato, per invitarlo a non arrendersi. Tale tecnica, conosciuta come cifratura di Cesare consiste nel mettere in corrispondenza le lettere dell’alfabeto con le stesse lettere spostate di un certo numero di posti, riportando le lettere avanzanti all’inizio. Supponiamo di voler inviare il messaggio segreto : ”Attaccheremo domani”. Per crittografare il messaggio usiamo l’alfabeto cifrante scritto di seguito
Il messaggio cifrato
risulterà essere “ TPPTVVDANAGI ZIGTHE”
e L’uso della crittografia ha avuto particolare importanza durante la seconda guerra mondiale, specialmente da parte dei tedeschi. Un loro scienziato, Artur Scherbius, aveva ideato una macchina passata alla storia con il nome significativo di “Enigma” in grado di cifrare in modo complesso i messaggi usando una cifratura tipo quella di Cesare, però variabile in continuazione.
( La macchina “Enigma” di circa 12 Kg di peso come si presentava, a sinistra, e i dischi usati per la codifica, a destra, che venivano scambiati in continuazione). Il criterio della variabilità era particolarmente importante perché i decrittatori non facevano in tempo a scoprire il codice utilizzato di volta in volta. Ci volle tutto l’ingegno di alcuni scienziati polacchi con il loro progetto “Bomba” per dare un primo colpo al sistema segreto tedesco che fu definitivamente smantellato, spostando forse le sorti della guerra a favore degli alleati, per opera di scienziati inglesi diretti da Alan Turing, ideatore dei processi algoritmici e precursore dell’intelligenza artificiale, ipotizzata e studiata da Turing prima ancora che i computer avessero pratica realizzazione. Tutti questi esempi mettono in evidenza come le tecniche crittografiche si siano sviluppate di pari passo con lo sviluppo tecnologico, e naturalmente ne esistono molte altre anche estremamente complesse. Oggi esse assumono una importanza ancora maggiore, visto lo sviluppo di internet e dell’ E-commerce, l’acquisto di merci o altro attraverso la rete del Web. Il problema naturalmente non è solo quello relativo alla privacy, nelle nostre E-mail ad esempio, ma è quello della segretezza quando si trasmettono dati relativi a carte di credito e conti bancari o postali. Nel 1977 tre matematici del prestigioso “Mit”, Ronald Rivest, Adi Shamir e Leonard Adleman, idearono una tecnica crittografica che prese il nome di RSA, acronimo dei loro cognomi. Tale tecnica estremamente sicura in quanto difficilmente decodificabile, che risulta oggi una delle più diffuse, consegnò alla storia della scienza i loro nomi, oltre a renderli naturalmente ricchi, a dimostrazione di come anche la matematica, che appare come una scienza puramente speculativa, possa trovare applicazioni pratiche e redditizie. Il sistema RSA viene anche denominato “cifrario a chiave pubblica”, in contrapposizione al “cifrario a chiave privata”, ma vediamo di capire meglio. La tecnica di crittazione corrisponde al cifrario (ad esempio la cifratura di Cesare), il metodo usato per la cifratura è la chiave ( di quanti posti devono essere spostate le lettere). Possiamo pensare, per semplificare il discorso, ad un cofanetto contenente il messaggio, chiuso da un lucchetto. Quando si vuole spedire un messaggio lo si chiude a chiave nel cofanetto. Chi lo riceve, o lo intercetta, non può aprirlo a meno di avere una copia della chiave o di ricevere dal mittente, attraverso una spedizione parallela, la copia di essa . Va da se che questo sistema, metaforico naturalmente, non è molto sicuro perché si potrebbe intercettare la chiave spedita per vie parallele. Si potrebbe usare un altro metodo in alternativa: chiudere il cofanetto e spedirlo. Chi lo riceve non lo apre, ma aggiunge un altro lucchetto di cui lui solo ha la chiave e rispedisce il cofanetto al mittente. Il mittente, a sua volta, quando riceve indietro il cofanetto toglie il suo lucchetto e lo rimanda di nuovo al destinatario che potrà tranquillamente aprirlo senza che altri possano farlo. Questo sistema prevede l’utilizzo di due chiavi diverse in possesso solo di chi trasmette (la chiave di codifica, ) e di chi riceve (la chiave di decodifica), “chiavi private, appunto”. Nel sistema “a chiave pubblica”, invece, si mette a disposizione di chiunque rendendole pubbliche quindi, il sistema di cifratura e la chiave per crittare i messaggi, in modo che chiunque possa scrivere messaggi crittati, ma solo chi ha reso pubblici quei dati può decrittarli, perché solo lui conosce tale chiave che resta naturalmente segreta. Nemmeno chi esegue la codifica sarebbe in grado di decodificarlo, se ne dimenticasse il contenuto, perché la chiave di decodifica non è in suo possesso. La domanda a questo punto è d’obbligo:”Cosa rende questo sistema così sicuro ?”. La risposta è nella matematica, e in particolare in alcune proprietà caratteristiche dei numeri primi, che cercherò di illustrare. Prima però dovremmo analizzare un particolare sistema di conteggio che in realtà già utilizziamo senza accorgercene, che chiamerò sistema “orologio”. Se consideriamo il quadrante dell’orologio, quello tondo con 12 ore e la lancetta, tanto per intenderci, vediamo che dopo un giro completo la lancetta tornerà ad indicare la stessa ora (Tralasciamo la distinzione fra mattino e pomeriggio). Aggiungendo 7 ore alle 8 , la lancetta indicherà il numero 3. Ebbene nel sistema di conteggio ad “orologio” quello che conta non è il risultato delle operazioni (8+7=15), ma la posizione finale della lancetta. Nel caso appena detto diciamo che il risultato della operazione 8 + 7 = 15 è 15 (Modulo 12) = 3 Questo modo di operare viene detto di tipo modulare, intendendo per modulo il numero di ore del nostro “orologio”, e non si applica solo alla somma ma a qualunque tipo di operazione. Così: 5*7 = 35 e 5*7 (Modulo 12) = 11 ( la lancetta compie due giri completi più 11 ore, a partire da 0 ovvero da 12); 34 = 81 e 34 (Modulo 12) = 9 (sei giri completi della lancetta più 9) ; 38 – 34 = 4 e 4 (Modulo 12) = 4 (la lancetta è tornata indietro di due giri completi più 10 a partire, però, dalle 2. Infatti 38(Mod. 12) = 2). E naturalmente 24*7 = 168 e quindi 24*7 (Mod.12) = 0 perché la posizione sulle dodici equivale a zero ( la lancetta compie 14 giri completi, partendo da 0). Questo tipo di conteggio, ideato da Gauss, può essere utilizzato con qualunque modulo si voglia assumere, utilizzando “orologi” con un numero qualsiasi di ore. Ad esempio: 27*6 = 162 e dunque 27*6 (Mod.15) =12 o anche 27*6 (Mod.8) =2; 345 = 45435424 così che 345 (Mod.22) = 12 oppure utilizzando un altro modulo 345 (Mod.1826) = 892; 37*58 =2146 e allora 37*58 (Mod.237) = 13. Come si può notare il risultato di queste operazioni, anche per numeri grandissimi, è sempre minore del numero assunto come modulo. Potrebbe sembrare complicato operare con numeri molto grandi, ma il valore finale si ottiene semplicemente dividendo il numero ottenuto come risultato dell’operazione per il valore del modulo, e prendendo solo il resto:15/12=1 con resto 3 ; 35 / 12 = 2 con resto di 11; 81/12 = 6 con resto 9; 4 / 12 = 0 con resto 4; 168 / 12 = 14 con resto 0; 162 / 15 = 10 con resto 12; e per completare tutti gli esempi riportati 45435424 / 22 = 2065246 con resto 12; 2146 / 237 = 9 con resto 13. In termini più strettamente matematici esprimere un numero N in un qualunque modulo M equivale a trovare due numeri interi x e r, tali che: N = M * x + r (relazione 1) dove x è il risultato della divisione ed r il suo resto che sarà il valore che a noi interessa, entrambi interi. Un metodo ricorsivo, sviluppabile con un semplice programmino al computer, consiste nel sottrarre M da N e ripetendo il procedimento fino ad ottenere come risultato un numero minore di M che sarà il nostro r. Il valore di x non è altro che il numero di sottrazioni effettuate, ma non è importante.
Due numeri diversi A e B che espressi con lo stesso modulo danno lo stesso risultato di definiscono “congrui” secondo quella base. Per esempio: 22 (Mod. 15) = 7 e 37 (Mod 15) = 7 e allora si può scrivere 22 ≡ 37 (Mod. 15) intendendo con questa scrittura esprimere la congruenza fra i due numeri. Il concetto di congruenza nell’algebra modulare, quella delle operazioni ad “orologio” appena descritto, equivale al concetto di uguaglianza che utilizziamo nell’algebra normale. Fin qui niente di particolarmente utile, almeno apparentemente. L’importanza della rappresentazione di tipo modulare si manifesta però quando entriamo nel campo dei numeri primi. I numeri primi, come si ricorderà, sono tutti quei numeri divisibili solo per 1 e per se stessi, ed hanno molte caratteristiche particolari che li rendono utili per la costruzione della crittografia a chiave pubblica. La prima cosa da ricordare, memori dei trascorsi scolastici di media inferiore, è che qualunque numero è scomponibile in fattori primi, cioè è esprimibile come prodotto di numeri primi elevati ad opportune potenze. Possiamo scrivere ad esempio: 36 = 22*32 ; 30 = 2*3*5 ; 132 = 22*3*11 ; 37= 37 Due numeri qualunque, poi, x e y si definiscono “coprimi”, o anche si dice che x è primo con y, se i due numeri non hanno divisori comuni, cioè se nella scomposizione in fattori primi dei due numeri non compaiono fattori uguali. x = a1n1*a2n2*a3n3*……*aknk e y =b1m1*b2m2*b3m3*….*bkmk x e y risultano “coprimi” se tutte le ah sono diverse dalle bh, indipendentemente dal valore delle nh e delle mh per i quali non c’è limitazione. Abbiamo allora che 36 = 22*32 è “coprimo” con 25 = 52 ( Nella scomposizione non ci sono termini uguali) ma non con 132 = 22*3*11 ( compaiono in entrambe le scomposizioni sia 2 che 3, e non hanno importanza le potenze). Per trovare un numero x che sia primo con un numero dato y, cioè che i due numeri siano “coprimi”, è sufficiente scomporre in fattori primi il numero y e calcolare il valore di x facendo il prodotto di uno o più numeri primi che non compaiono nella scomposizione di y stesso. Ad esempio per trovare un numero “coprimo” con 132 basta porre x = 7*5 =35 o x=52*13*17 = 5525 o anche semplicemente x = 7. Per continuare il discorso dobbiamo tener conto ora di due teoremi fondamentali, che ci serviranno in seguito, senza comunque addentrarci nelle dimostrazioni. Il primo è il piccolo teorema di Fermat il quale afferma che se prendiamo un numero primo p allora, per qualunque numero positivo M primo rispetto a p, ovvero “coprimo” con p, si ha: M (p-1) (Mod. p ) = 1 (relazione 2) questa si può anche scrivere, secondo la relazione 1, come M (p-1) = m*p + 1, con m intero. Ad esempio 64 (Mod 5) = 1, cioè 64=1296= 259*5 + 1 (5 è un numero primo e 6 è coprimo con 5). Oppure 310 (Mod 11) = 1, cioè 310= 59049 = 5368*11 + 1 (anche 11 è un numero primo e 3 è ad esso coprimo). 104 (Mod.5) = 10000 (Mod.5) = 0 (10 non è coprimo con 5 e la relazione non è soddisfatta). E’ sufficiente, in ogni caso, scegliere M < p, perché essendo p un numero primo, qualunque numero ad esso inferiore è coprimo con p stesso, non avendo sicuramente divisori comuni. E’ importante notare una notevole conseguenza della relazione 2. Per qualunque valore di k intero si ha infatti: M k*(p-1) (Mod. p ) = 1 ( relazione 3 ) La dimostrazione la si ottiene direttamente dalla relazione 2, se eleviamo alla potenza k entrambi i membri della stessa. (L’operazione di elevamento a potenza è lecita nelle operazioni di tipo modulare ed è soggetta alle stesse regole dell’aritmetica normale purchè si tenga conto della relazione 5, scritta in seguito, visto che l’operazione di elevamento a potenza non è altro che un prodotto). [M (p-1) (Mod. p )] k = 1k = 1 da cui M k*(p-1) (Mod. p ) = 1 L’altra relazione, derivante da questa, riguardante due numeri primi p e q e il loro prodotto n=p*q, fu scoperta da Eulero e afferma che dato un numero positivo qualunque M che sia primo relativo ad n, cioè “coprimo” con n, si ha sempre, per qualunque scelta di p e q: M (p-1)*(q-1) (Mod. n) = 1 (relazione 4) e di nuovo, in base alla relazione 1, abbiamo che M (p-1)*(q-1) = z*n + 1= z*p*q + 1. Possiamo di nuovo verificarlo prendendo ad esempio p = 3 e q = 7 per cui n = 7*3 =21; la relazione 4 assumendo M = 5 diventa in questo caso 5(3-1)*(7-1) (Mod.21) = 1. Dobbiamo allora calcolare 5(2*6) = 512 ; questo calcolo apparentemente complicato può essere risolto applicando semplici proprietà delle potenze, osservando che 512 = 5(3+3+3+3) = 53*53*53*53 . In definitiva la relazione 3 assume la forma 5(3-1)*(7-1) (Mod.21) = 512 (Mod.21) = 5(3+3+3+3) (Mod.21) = (53*53*53*53) Mod.21 = (125*125*125*125) (Mod.21) e osservando che 125(Mod.21) = 20 si può scrivere anche (125*125*125*125) (Mod.21) = (20*20*20*20) (Mod.21) = 160000 (Mod.21) = 1 e infatti 160000=21*7619 + 1 = 159999 + 1. Nel procedere nel calcolo si è sfruttata una delle proprietà del calcolo modulare, cioè dati due numeri qualunque x e y si ha che (x*y) (Mod z) = [x (Mod.z) * y (Mod.z)] (Mod.z) (Relazione 5) come si può facilmente verificare prendendo per esempio x=136, y=32 e z=29 e sviluppando: (136*32) (Mod. 29) = 4352 (Mod. 29) = 2 che si può scrivere anche: (136*32)(Mod. 29) = [136 (Mod. 29) * 32 (Mod. 29)] (Mod. 29) = = ( 20*3) (Mod. 29) = 60 (Mod. 29) = 2 Possiamo adesso descrivere la crittografia RSA. Il gestore delle chiavi opera in questa successione:
e*d [Mod (p-1)*(q-1)] = 1, che scritta in base alla relazione 1 assume la forma : e*d =k * [(p-1) * (q-1)] + 1; ed è facile da questa ricavare d conoscendo e, con k opportuno perché d deve risultare intero. Il gestore delle chiavi mette a disposizione di chiunque voglia mettersi in comunicazione con lui la “chiave pubblica” costituita dalla coppia di valori (n ; e) e tiene custodita la “chiave privata” costituita dalla coppia di numeri (n ; d) che solo lui conosce. La potenza del sistema sta nell’impossibilità di risalire ai numeri primi p e q che sono gli unici che permettono di calcolare e e d, quando sia noto n, in quanto i numeri usati sono enormi, cioè composti da centinaia di cifre. La sicurezza del sistema risiede proprio nel fatto che anche i computer più potenti impiegherebbero anni per scomporre n nell’unica combinazione possibile dei numeri primi usati per determinarlo. Una volta determinati i valori di n e e d , p e q diventano inutili e possono anche essere dimenticati, ma non divulgati. Invita , quindi, chiunque voglia mettersi in contatto con lui con un messaggio cifrato ad operare nel seguente modo: prendere il messaggio in chiaro m, qualunque esso sia, trasformarlo nel messaggio codificato c = me (Mod. n) e spedirlo . Quando riceverà il messaggio codificato c, per ottenere il messaggio in chiaro m, basterà fare la semplice operazione m = cd (Mod. n) che solo lui, però potrà fare in quanto unico possessore della chiave privata d.. Com’è possibile? Sappiamo che: cd (Mod. n) = (me)d (Mod. n) = m e*d (Mod. n) = m k[(p-1)*(q-1)] + 1 (Mod. n) . questa relazione deriva dalla scelta fatta per e e dal valore di e*d ; l’ultimo termine inoltre diventa m k[(p-1)*(q-1)] + 1 (Mod. n) = m k[(p-1)*(q-1)] *m1 (Mod. n) Per il teorema di Eulero, però, abbiamo anche visto
m (p-1)*(q-1) (Mod. n) = 1 e per la relazione 3 si ha anche m k[(p-1)*(q-1)] (Mod. n) = 1
Moltiplicando entrambi i membri per m si arriva alla conclusione:
m k[(p-1)*(q-1)] (Mod. n) * m1 = 1*m1 = m k[(p-1)*(q-1)] +1 (Mod. n) = cd (Mod. n) In definitiva cd (Mod. n) = m E’ importante ribadire che la sicurezza del sistema è affidata alla segretezza del codice privato che solo il gestore delle chiavi conosce e alla difficoltà della fattorizzazione di n che, come abbiamo detto, è estremamente difficile da realizzare. Si potrebbe obiettare che non è impossibile che qualcuno riesca a calcolare i valori di p e q visto che n è noto, riuscendo, quindi, a scardinare il sistema. La risposta è nei fatti. Si è calcolato che un computer in grado di eseguire un milione di istruzioni al secondo, per scomporre in fattori primi un numero di 129 cifre, impiegherebbe 5000 anni. Con lo sviluppo dei computer quantistici, in grado di operare con velocità enormemente più grandi, il sistema dovrà essere sicuramente rivisto. Ma questo lo dirà il futuro.
Domenico Di Bucchianico |
|||


 chi lo riceverà dovrà semplicemente fare la corrispondenza inversa.
Basta conoscere di quanti posti deve essere spostata la serie di
lettere. Questo sistema, però, è facilmente decrittabile anche se
non si conosce di quanti posti bisogna spostarsi, agendo
semplicemente per tentativi. Al massimo bastano 20 tentativi, nel
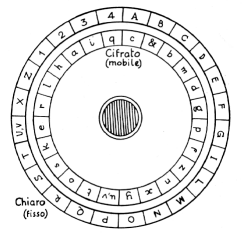
nostro caso. Leon Battista Alberti fu uno degli uomini più
importanti del Rinascimento, noto soprattutto come architetto; suo è
infatti il progetto di Santa Maria Novella in Firenze. In realtà fu
uomo poliedrico e si interessò di crittografia tanto da ideare un
dispositivo che eseguiva la cifratura di Cesare. Esso consisteva di
due dischi concentrici (figura a destra) su cui erano riportate le
lettere dell’alfabeto e i numeri. Ruotando uno dei dischi di quanti
passi si voleva, si avevano le corrispondenze per la cifratura, e
per la decifratura naturalmente.
chi lo riceverà dovrà semplicemente fare la corrispondenza inversa.
Basta conoscere di quanti posti deve essere spostata la serie di
lettere. Questo sistema, però, è facilmente decrittabile anche se
non si conosce di quanti posti bisogna spostarsi, agendo
semplicemente per tentativi. Al massimo bastano 20 tentativi, nel
nostro caso. Leon Battista Alberti fu uno degli uomini più
importanti del Rinascimento, noto soprattutto come architetto; suo è
infatti il progetto di Santa Maria Novella in Firenze. In realtà fu
uomo poliedrico e si interessò di crittografia tanto da ideare un
dispositivo che eseguiva la cifratura di Cesare. Esso consisteva di
due dischi concentrici (figura a destra) su cui erano riportate le
lettere dell’alfabeto e i numeri. Ruotando uno dei dischi di quanti
passi si voleva, si avevano le corrispondenze per la cifratura, e
per la decifratura naturalmente.