|
ITIS |
IstitutoTecnico
■
LiceoTecnologico Leonardo da Vinci ■ Lanciano |
 |
LSTS |
 L'angolo della scienza
L'angolo della scienza |
|||
|
Infinito, infiniti e paradossi dell’infinito. Si deve ad Anassimandro, un filosofo greco vissuto tra il 610 e il 546 a.c., l’introduzione del concetto di infinito in filosofia; il suo “apeiron” (apeiron) era il principio stesso di esistenza di ogni cosa. Il principio è stato poi ripreso da altri con accezioni e significati diversi.. “C'è un concetto che corrompe e altera tutti gli altri. Non parlo del Male, il cui limitato impero è l'Etica; parlo dell'Infinito”, così ha scritto J. L. Borges. Perciò parlare di infinito non è certo facile. Non l’infinità di spazio e tempo nel quale era dolce naufragare per Leopardi, né tantomeno l’infinito dell’Assoluto Divino, sui quali sono stati scritti un’infinità di testi, tanto per restare in tema, ma il senso dell’infinito che si ha in matematica e in geometria. In particolare per la matematica, abituata a trattare entità ben definite, parlare di enti “in-definiti” o “in-determinati”, “infiniti” appunto, assume un particolare significato. Se provate però a rispondere alla domanda “Quanti sono i numeri interi?”, la risposta verrà quasi inconsciamente e immediatamente associata all’infinito. Una storiella di Cesare Zavattini, famoso sceneggiatore cinematografico, scrittore e poeta italiano, così affronta il problema in un racconto tutto imperniato sull’ironia dal titolo :”Gara di matematica”. E’ un ricordo della mia infanzia. Abitavo a Gottinga nel dicembre del milleottocentosettanta. Mio padre ed io giungemmo all’Accademia quando il presidente Maust stava cominciando l’appello dei partecipanti alla Gara Mondiale di Matematica. Subito babbo andò a mettersi fra gli iscritti dopo avermi affidato alla signora Katten, amica di famiglia. Seppi da lei che il colpo del cannone di Pombo, il bidello, avrebbe segnato l’inizio della storica contesa. La signora Katten mi raccontò un episodio, ignoto ai più, intorno all’attività di Pombo. Costui sparava da trent’anni un colpo di cannone per annunciare il mezzogiorno preciso. Una volta se n’era dimenticato. Il dì appresso, allora, aveva sparato il colpo del giorno prima, e così di seguito fino a quel venerdì del milleottocentosettanta, Nessuno a Gottinga si era mai accorto che Pombo sparava il colpo del giorno avanti. ”Esauriti i preliminari, la gara ebbe inizio alla presenza del principe Ottone e di un ragguardevole gruppo di intellettuali. “Uno, due, tre, quattro, cinque… Nella sala si udivano soltanto le voci dei gareggianti. “Alle diciassette circa, avevano superato il ventesimo migliaio. Il pubblico si appassionava alla nobile contesa e i commenti si intrecciavano. Alle diciannove, Alain, della Sorbona, si accasciò sfinito. “Alle venti, i superstiti erano sette. ”36767, 36768, 36769, 36770…” “Alle ventuno Pombo accese i lampioni. Gli spettatori ne approfittarono per mangiare le provviste portate da casa. “40719, 40720, 40721…” “Io guardavo mio padre, madido di sudore, ma tenace. La signora Katten accarezzandomi i capelli ripeteva come un ritornello: ’Che bravo babbo hai,’ e a me non pareva neppure di avere fame. Alle ventidue precise avvenne il primo colpo di scena: l’algebrista Pull scattò: “Un miliardo”. “Un oh di meraviglia coronò l’inattesa sortita; si restò tutti col fiato sospeso. “Binacchi , un italiano, aggiunse issofatto: “’Un miliardo di miliardi di miliardi.’ Nella sala scoppiò un applauso subito represso dal Presidente. Mio padre guardò intorno con superiorità, sorrise alla signora Katten e cominciò: “’Un miliardo di miliardi di miliardi di miliardi di miliardi di miliardi di miliardi di miliardi di miliardi di miliardi di miliardi di miliardi di miliardi di miliardi di miliardi di miliardi di miliardi…’ “La folla delirava: ‘Evviva, evviva. ’“La signora Katten e io, stretti uno all’altro, piangevamo dall’emozione. “…di miliardi di miliardi di miliardi di miliardi di miliardi di miliardi.’ “Il presidente Maust, pallidissimo, mormorava a mio padre, tirandolo per le falde della palandrana: ’Basta, basta, le farà male.’ Mio padre seguitava fieramente: “… di miliardi di miliardi di miliardi di miliardi.’ A poco a poco la sua voce si smorzò, l’ultimo fievole di miliardi gli uscì dalle labbra come un sospiro, indi si abbattè sfinito sulla sedia. Gli spettatori in piedi lo acclamavano freneticamente. Il principe Ottone gli si avvicinò e stava per appuntargli una medaglia sul petto quando Gianni Binacchi urlò: “’Più uno!’ “La folla precipitatasi nell’emiciclo portò in trionfo Gianni Binacchi. Quando tornammo a casa, mia madre ci aspettava ansiosa alla porta. Pioveva. Il babbo, appena sceso dalla diligenza, le si gettò tra le braccia singhiozzando: ‘Se avessi detto più due avrei vinto io.’” (Cesare Zavattini - I tre libri, Parliamo tanto di me - Bompiani - cap. XVI pag. 48,49,50) Come si può notare il concetto di infinito è associato al numero, cioè al processo del contare. E infatti dato un numero se ne può pensare uno più grande, così come si può prolungare una retta aggiungendo punti ai suoi estremi. Allo stesso modo si può parlare di infinitesimi dividendo un segmento in parti più piccole, in un procedimento senza fine. Aristotele (384-322 a.c.) parlava a questo riguardo di “Infinito potenziale”, rifiutandosi di accettare l’idea dell”infinito attuale”, della totalità intesa come singola entità, inaccessibile alla mente umana. L’”infinito potenziale” è una sorta di scappatoia che ci libera da ogni problema; quando ne abbiamo bisogno possiamo aumentare quel che ci serve: un numero, un’area, un volume, senza limiti. Lo utilizzò ad esempio Archimede (287-212 a.c.) con il metodo di “esaustione” inventato da tale Eudosso da Cnido (408-355 a.c.). Come calcolare l’area del cerchio? Si costruiscono due poligoni regolari uno circoscritto ed uno inscritto alla circonferenza. L’area del poligono circoscritto è maggiore di quella del cerchio, mentre l’area del poligono inscritto è inferiore ad essa. Aumentando il numero dei lati le due aree tenderanno sempre più ad avvicinarsi a quella del cerchio.
Questo metodo permise ad Archimede di predire che il valore di Pigreco doveva essere compreso fra 3 + 10/71 e 3 + 1/7. Possiamo considerarlo una anticipazione del metodo di analisi infinitesimale introdotto da Cavalieri (1598-1647) agli inizi del ‘600, mediante il quale possiamo pensare aree e volumi come fette di curva di spessore infinitesimo, cioè piccolo a piacere, che sovrapposte danno l’area o il volume totali. In ogni caso, potenziale o attuale che sia, il concetto di infinito costringe la mente a peripezie non indifferenti a causa dei paradossi che incontriamo nel suo utilizzo. Uno dei più noti paradossi fu senz’altro quello prospettato dal filosofo Zenone (495-430 a.c.). Secondo Zenone una freccia scoccata da un arciere non raggiungerà mai il bersaglio, e non si muoverà nemmeno. Per colpire il bersaglio la freccia dovrà percorrere prima metà percorso, ma per arrivare a metà percorso dovrà volare prima per 1/4 del percorso, la metà della metà, e prima ancora dovrà percorrere 1/8 del percorso, e così via.. Poiché il processo di suddivisione può continuare all’infinito, ogni singolo passetto della freccia sarà nullo. Se ogni singolo passetto fosse diverso da zero la loro somma di termini infiniti dovrebbe risultare infinita, il che sarebbe assurdo. La conclusione secondo Zenone è che il movimento della freccia è puramente illusorio. Il paradosso di Achille e la tartaruga porta alla stessa conclusione. Nella leggendaria sfida di Achille e la tartaruga, questa seconda, partendo in anticipo, non verrà mai raggiunta. Dovremo arrivare al diciottesimo secolo per arrivare a scoprire che una somma di infiniti termini può risultare finita. Un altro problema logico che l’uso dell’infinito ci costringe ad affrontare risale a Galileo. Egli si chiedeva quanti fossero i quadrati dei numeri interi. La sua risposta fu che erano infiniti quanto i numeri stessi. Si possono infatti mettere in corrispondenza biunivoca, uno a uno per capirci, i numeri interi ed i loro quadrati secondo la corrispondenza sotto riportata. 1 2 3 4 5 6 7 8 9 10 11 …..
1 4 9 16 25 36 49 64 81 100 121 ….. Galileo risolse il problema facendo finta di nulla. Eppure i quadrati sono meno dei numeri interi, essendo una parte di essi. Si arriva alla conclusione che il tutto contiene gli stessi elementi di una sua parte. Una pura eresia per i filosofi classici, per i quali una parte deve sempre essere inferiore al tutto. Allo stesso modo si può dimostrare che i numeri pari o i numeri dispari sono infiniti, e anche i numeri primi, come ebbe a dimostrare Eulero (1707-1783), ecc..ecc... Proviamo a guardare un altro aspetto, considerando le cosiddette serie numeriche, cioè la somma di infiniti termini costruiti secondo un procedimento iterativo. Ad esempio la serie che segue che si costruisce assegnando ad n successivamente tutti i possibili valori interi positivi:
Posiamo a dimostrare che essa è convergente, cioè il suo risultato è finito. (Ricordo che esistono serie divergenti nelle quali il risultato della somma è infinito). Indichiamo con S il risultato di tale somma, ammettendo che esista e sia finita, allora possiamo scrivere: S = 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + …= 1/2 + (1/4 + 1/8 + 1/16 + 1/32 + …..) abbiamo semplicemente utilizzato delle parentesi, quindi rimane tutto inalterato. Mettiamo adesso in evidenza 1/2 tra tutti gli elementi racchiusi dentro parentesi e vediamo che resta, dentro parentesi, la serie iniziale. S = 1/2 + 1/2 *(1/2 +1/4 + 1/8 + 1/16 + 1/32 + …..) = 1/2 + 1/2 *S La soluzione di questa semplice equazione di primo grado ci fornisce S = 1, con buona pace di Zenone. Proviamo ad applicare lo stesso metodo alla serie, piuttosto strana per la verità, S = 1-1+1-1+1-1+1-1+1-1+1-…. Riscriviamo la stessa serie raccogliendo: S = 1- (1-1+1-1+1-1+1-1+1-1…….) = 1 – S Anche questa è facilmente risolvibile e fornisce come soluzione S = 1/ 2. e questo risultato farebbe già storcere il naso, perché prendendo i termini a coppie avremmo una somma di zeri: S = (1-1)+(1-1)+(1-1)+(1-1)+(1-1)…….+(1-1).. E non basta. Se raggruppiamo i numeri in modo diverso ad esempio prendendo due termini di posto dispari e uno di posto pari cioè 1 3 2 5 7 4 9 11 6….otteniamo S = ( 1+1-1)+(1+1-1)+(1+1-1)+(1+1-1)+….= 1+1+1+1+1+1+1… Il risultato di tale somma è infinito. Allo stesso modo posso ottenere un qualunque risultato; prendendo ad esempio i termini nelle posizioni 1 3 5 2 7 4 9 6 11 8 13 10 15 12 17 la somma diventa S = 1+1+1+(-1+1)+(-1+1)+(-1+1)+(-1+1)+….= 3+0+0+0+0+0+0…..
Paradossi dell’infinito, risolti assumendo criteri che impediscono di invertire i termini di una serie, in particolare in presenza di termini negativi. (Per inciso, la serie scritta è indeterminata). Un altro paradosso associato all’infinito si deve ad Hilbert (1862-1943) e va sotto il nome di “Albergo di Hilbert”. In un albergo normale con un numero di stanze finito, tutte occupate, è impossibile ospitare un eventuale ospite ulteriore. Ma se l’albergo ha un numero di stanze infinito allora possiamo fare una semplice operazione di spostamento, mettendo gli ospiti ognuno nella stanza successiva, liberando così la prima. E anche se dovessimo trovare posto ad un infinito numero di nuovi avventori, potremmo tranquillamente spostare tutti i presenti nelle stanze dispari, liberando tutte le pari, risolvendo il problema. Un altro paradosso, più letterario questa volta, viene attribuito allo scrittore Laurence Sterne (1713-1768). Oltre a diverse innovazioni letterarie di carattere provocatorio nella sua “Vita e opinioni di Tristram Shandy, gentiluomo”, di cui voleva scrivere la biografia. Il romanzo descrive dettagliatamente tutti gli avvenimenti della vita di Shandy a cominciare dal suo concepimento, e dopo molti capitoli, costati anni di lavoro, descrive solo i primi due giorni di vita del protagonista.. E’ evidente che in una vita comune e mortale l’autore a quel ritmo non sarebbe mai riuscito a completare il romanzo. Ma se si potesse supporre una vita infinita? Allora le cose sarebbero diverse e lo scrittore potrebbe scrivere tutta la biografia. Come sarebbe possibile? In realtà in questo esempio come in quello dell’albergo di Hilbert non stiamo facendo altro che giocare con il principio di corrispondenza biunivoca di cui abbiamo parlato. Ogni successione numerica infinita può essere posta in corrispondenza biunivoca con i numeri naturali. Così i giorni di scrittura possono essere messi in corrispondenza biunivoca con i giorni di vita, anche se ne sono solo una parte, perché l’infinito diventa “ciò che può essere posto in corrispondenza biunivoca con una sua parte”. Questa definizione introdotta da Dedekind (1831-1916) ha portato Georg Cantor (1845-1918) a lavorare in maniera sistematica con gli infiniti, affermando che esistono infiniti infiniti di “cardinalità” diversa. In realtà per non creare problemi di tipo religioso Cantor ha chiamato i suoi infiniti: “transfiniti”.
E le frazioni? Cioè i numeri razionali sono tanti quanto i numeri naturali? Certo rispose Cantor, basta disporre le frazioni in righe e colonne, di numero infinito, mettendo ad ogni rigo le frazioni con numeratore corrispondente al suo numero naturale, ed in ogni colonna le frazioni con denominatore corrispondente ad ogni numero naturale. Si ha allora:
E così è stabilita una corrispondenza fra le frazioni e i numeri naturali derivanti dal conteggio, quindi la “cardinalità” o “potenza” è la stessa. Cantor escogitò anche una algebra dei “transfiniti”, per cui si può scrivere:
Le formule appena scritte affermano semplicemente che sommando 1 ad infinito, il risultato è sempre infinito; sommando N ad infinito si ha infinito; ma anche sommando infinito ad infinito. La meraviglia nasce quando si fa il prodotto di due infiniti. Possiamo, però, ragionare come per le frazioni ponendo in righe e colonne semplicemente i numeri naturali ed individuando ogni elemento del prodotto con gli indici riga*colonna. Procedendo a zig zag come per le frazioni si trova la corrispondenza biunivoca fra il risultato del prodotto ed i numeri naturali. Cantor volle fare ancora un passo in avanti. Cosa possiamo dire dei numeri reali, cioè dei numeri decimali, sia quelli razionali che quelli irrazionali?. In particolare cerchiamo la risposta alla domanda: “Quanti sono i numeri decimali, ad esempio quelli compresi fra 0 e 1?”. Cantor rispose con una dimostrazione per assurdo universalmente conosciuto come “metodo diagonale di Cantor”. Il suo ragionamento fu il seguente. Supponiamo di essere in grado di scrivere tutti i numeri decimali compresi fra 0 e 1; essi saranno della forma 0,154367823739…. con un numero finito o infinito di cifre ( questo non ha importanza perché anche se le cifre dopo la virgola sono finite possiamo aggiungere tutti gli 0 che vogliamo, anche infiniti 0). Li possiamo scrivere disponendoli uno per rigo, in corrispondenza biunivoca con i numeri interi, ipotizzando così che siano numerabili. 1 - 0,66342528173635328282650024….. 2 - 0,12453339286547121930000000….. 3 - 0,23861432574947358816354379….. 4 - 0,00002664417728355383883800….. 5 - 0,23459726245353272767353723….. 6 - 0,11526283365437893663738328….. ………………………………………….. Consideriamo
adesso il numero costruito prendendo le prima cifra dopo la virgola
dal primo numero, la seconda dopo la virgola dal secondo numero, la
terza dal terzo numero e così via, tutti gli elementi della
diagonale insomma, aumentati tutti, per esempio di 1, ponendo 0
quando essa è 9. Ebbene questo nuovo numero,
0,739103……o
altri costruiti aggiungendo 2 o 3 o la cifra che vogliamo, non è
compresa nell’elenco fatto. Esso differisce dal primo numero per la
prima cifra dopo la virgola, dal secondo numero per la seconda cifra
dopo la virgola, dal terzo per la terza cifra e così via. La
conclusione è che non è possibile scrivere tutti i numeri compresi
fra 0 e 1, e quindi sono “non numerabili”. Essi hanno una
“cardinalità” maggiore di
Cantor volle stupire ancora di più considerando un insieme di elementi di lunghezza nulla che contenesse elementi della stessa “cardinalità” del continuo. Questo insieme detto appunto “insieme di Cantor” è un sottoinsieme di un segmento costruito con un metodo iterativo di tipo frattale. Dato un segmento di lunghezza unitaria, dividiamolo per 3 e togliamo da esso la terza parte centrale. Resteranno due segmenti di lunghezza 1/3 agli estremi. A questi due segmenti tolgo ancora la terza parte centrale, e così via ripetendo lo stesso procedimento per tutti i segmenti rimanenti che saranno di lunghezza sempre più piccola. Ripetendo all’infinito questo procedimento avremo una serie di punti, e numeri naturalmente, costituiti dagli estremi dei vari segmenti rimanenti; ogni volta che tolgo il terzo centrale questi rimangono.
Quale sarà la misura x complessiva dei numeri rimanenti? La riposta è stupefacente :”Zero!” Si può calcolarla facendo la differenza fra la lunghezza del segmento iniziale, 1, e tutti i vari segmenti che si vanno sottraendo. Scriviamo allora, ricordando che la prima volta togliamo un terzo, poi due volte un terzo di un terzo e poi quattro volte un terzo di un terzo di un terzo e così via: x = 1 – 1/3 – 2 * ( 1/9 ) – 4 * ( 1/27 ) – 8 * ( 1/81)…… Con semplici passaggi matematici, e ricordando il risultato di una serie nota, si ha: x
= 1 –
x = 1 –
Il nostro insieme allora ha lunghezza 0, e quanti punti contiene? Con un geniale ragionamento, rappresentando i numeri in base 3, invece che in base 10, Cantor dimostrò, contrariamente a quanto ci si potrebbe aspettare, che i numeri di tale insieme costituivano una infinità non numerabile, della stessa potenza del continuo. Basta osservare che in base 3 i numeri decimali si scrivono nella forma 0,abcd..3 ( Per trasformare tale numero nella consueta base decimale che utilizziamo di solito, bisogna fare la operazione a*3-1+b*3-2+c*3-3… con a, b, c ecc. che possono assumere solo valore 0, 1 o 2). Ora i numeri compresi fra 1 e 1/3 sono del tipo 0,0..3, quelli compresi fra 1/3 e 2/3 sono del tipo 0,1..3. e quelli compresi fra 2/3 e 1 sono del tipo 0,2..3. Allo stesso modo si può vedere che i numeri compresi fra 0 e 1/9 sono del tipo 0,00..3, quelli fra 1/9 e 2/9 sono del tipo 0,01..3. e quelli compresi fra 2/9 e 3/9=1/3 sono del tipo 0,02..3. I numeri compresi fra 1/3 e 4/9 sono del tipo 0,10..3, quelli compresi fra 4/9 e 5/9 sono del tipo 0,11..3 e quelli compresi fra 5/9 e 6/9=2/3 sono del tipo 0,12..3. E così via. Se si osserva attentamente, le parti centrali di ogni segmento rimanente contengono degli 1, come cifra dopo la virgola, mentre le parti estreme contengono solo degli 0 e 2. Nel costruire il nostro sottoinsieme, però noi togliamo sempre la parte centrale, quindi vanno eliminati tutti i termini con degli 1 dopo la virgola. (C’è solo una piccola precisazione da fare: la frazione 1/3 in base 3 corrisponde a 0,13, così come 1/9 corrisponde a 0,013, ad esempio. Ma questi numeri si possono anche scrivere rispettivamente 0,0222222…3 e 0,0022222…3 con infiniti 2). Gli elementi che costituiscono l’insieme di Cantor sono quindi termini del tipo 0,020222022… ed essi hanno la stessa potenza del continuo, cioè la stessa “cardinalità”; infatti cambiando tutti i 2 con 1 otteniamo tutti i possibili numeri compresi fra 0 e 1, espressi in base 2. Un insieme di elementi della stessa potenza del continuo, la cui somma è 0. Un risultato veramente sconcertante, paradossale, appunto. Egli passò poi
ad analizzare la “cardinalità” dello spazio bidimensionale.
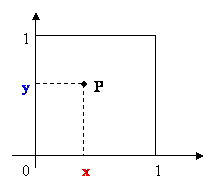
Prendiamo un quadrato di lato 1. E’ evidente che su ogni segmento
compreso fra 0 e 1 costituente il lato avremo un numero di punti con
la “cardinalità” del continuo, come appena visto. Ogni punto del
quadrato sarà individuato dalle sue coordinate. Ad esempio il punto
caratterizzato da una ascissa x =
0,4367514321.. ed una
ordinata y = 0, 7672432127….
P = 0, 47366772541342312217…….
Cantor faceva notare
che questa rappresentazione apparteneva al continuo, per cui ne conc
P = 0, 842253437591326864………
Lo stesso Cantor ne rimase sorpreso, tanto da affermare in una corrispondenza : “Lo vedo ma non ci credo!”. Utilizzando l’aritmetica dei “transfiniti” possiamo allora scrivere relazioni paradossali quali: C
+
Risultati veramente sorprendenti. Cantor cercò anche, per il resto della vita, di dimostrare se esistesse un insieme di potenza intermedia fra i numeri razionali ed il continuo, senza però riuscirci, ed il problema è ancora irrisolto. Egli fece poi un ulteriore salto considerando un nuovo tipo di oggetti: gli insiemi; e infatti la teoria degli insiemi ebbe da lui origine. Cantor fu il primo a intuire ed affermare che gli insiemi infiniti possono avere diverse grandezze o “cardinalità”, un autentico colpo per la logica. Dato un qualsiasi insieme I, infatti, esiste sempre l'insieme di tutti i possibili sottoinsiemi di I, chiamato da lui insieme potenza di I. Ad esempio prendiamo un insieme composto da soli {1, 2 , 3}. Possiamo considerare ora tutti i sottoinsiemi ottenibili da esso, a partire dall’insieme vuoto, cioè privo di elementi: { },{1},{2},{3},{1;2},{1;3},{2;3},{1;2;3} Cantor dimostrò che l'insieme potenza di un insieme I contiene più elementi di I stesso, in particolare trovò che se I contiene m elementi, l’insieme di potenza di I contiene 2m elementi. E’ facile verificarlo nell’esempio appena fatto in cui m=3 e quindi 23 = 8. E’ il teorema di Cantor. Egli dimostrò, con un argomento del tipo diagonale usato per dimostrare la non numerabilità dei numeri reali, che questo era valido anche per insiemi che contenevano infiniti elementi, e che l’insieme potenza ha sempre una “cardinalità” maggiore dell’insieme di partenza. Dunque esiste una gerarchia infinita di “potenza” di insiemi infiniti, dalla quale sorgono i numeri “transfiniti”, e la loro peculiare aritmetica, perché da un insieme si può costruire un insieme potenza di “cardinalità” sempre maggiore e così all’infinito. Infiniti che nascono l’uno dall’altro, come in un gioco di scatole cinesi, e ognuno più “grande” degli altri. Questo portò un altro geniale matematico, David Hilbert (1862-1943), ad affermare: “Nessuno ci scaccerà dal paradiso che Cantor ha creato per noi”. Ma quando sembrava che tutto andasse per il meglio, un nuovo paradosso scoperto da Bertrand Russell (1872-1943), e che porta il suo nome, diede un colpo letale alle capacità psichiche di Cantor, provocandogli una crisi nervosa che lo porterà a terminare i suoi giorni in un ospedale psichiatrico. Il paradosso di Russell, è anche noto come il paradosso del barbiere. In un villaggio c’è un solo barbiere che fa la barba a tutti coloro che non si fanno la barba da soli, e solo a loro. La domanda è : “Chi rade il barbiere?”. Nasce un irrisolvibile paradosso perché da barbiere potrebbe radere se stesso ma non può farlo perché si raderebbe da solo e lui rade solo chi non si rade da solo, contraddicendo la premessa, e da cliente non potrebbe andare dal barbiere perché si fa la barba da solo. Questo paradosso, innocuo fino a quando si parla di barbieri, ebbe effetti devastanti sulla teoria degli insiemi, quando Russell propose particolari insiemi che non sono elementi di se stessi. Tutto un castello di premesse fatto di idee di insiemi di tipo intuitivo venne a cadere. La logica matematica, basata su costrutti logicamente coerenti e sulla quale stavano lavorando molti studiosi all’epoca, ne subì serie conseguenze tanto che molti interruppero le loro ricerche. Un famoso filosofo dell’epoca, Gottlob Frege (1848-1925), nel pubblicare il suo lavoro in cui cercava di ridurre la matematica e l’aritmetica ad una serie di assiomi basati solo sulla logica, fu costretto ad aggiungere una nota in cui dichiarava il proprio fallimento. Domenico Di Bucchianico |
|||

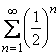 =
1/2 + 1/4 + 1/8 + 1/16 + 1/32 + ….. .
=
1/2 + 1/4 + 1/8 + 1/16 + 1/32 + ….. .  Tutti gli infiniti che si possono mettere in corrispondenza
biunivoca con i numeri naturali sono stati definiti da Cantor di
“cardinalità”
Tutti gli infiniti che si possono mettere in corrispondenza
biunivoca con i numeri naturali sono stati definiti da Cantor di
“cardinalità”
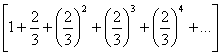 =
=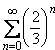 =
1 –
=
1 –
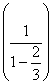 =
1 –
=
1 –
 Possiamo
allora associare a tale punto P il numero ottenuto prendendo le
cifre decimali di x e y e alternandole, cioè:
Possiamo
allora associare a tale punto P il numero ottenuto prendendo le
cifre decimali di x e y e alternandole, cioè: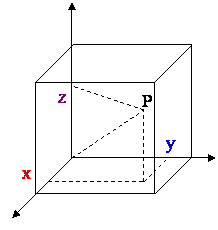 ludeva
che la “cardinalità” di
ludeva
che la “cardinalità” di