|
ITIS |
IstitutoTecnico
■
LiceoTecnologico Leonardo da Vinci ■ Lanciano |
 |
LSTS |
 L'angolo della scienza
L'angolo della scienza |
|||
|
Invenzione o scoperta? Nel 2000 una conferenza sull’importanza della matematica a cui partecipavano i più grandi scienziati in questo campo, veniva aperta con queste parole. “Il linguaggio dei numeri sta influenzando sempre di più la vita intorno a noi. Noi comunichiamo con i numeri. Ci parlano della nostra storia e del nostro futuro, come riusciamo a capire la natura. I numeri consentono agli scienziati di mettere a punto idee sul mondo che sarebbero indescrivibili senza i numeri. Ma i numeri sono un concetto inventato da noi o sono qualcosa che è sempre esistito indipendentemente da noi? O sono un linguaggio naturale dell’universo?”. Tutti siamo abituati a chiamare le nozioni matematiche o le formule, se vogliamo, con il nome dello studioso che se ne è occupato per prima, consegnandole alla storia. Si parla infatti del “teorema di Pitagora”, del “teorema di Talete”, del “teorema di Cantor” o del “teorema di Gödel”. (Ho voluto citare gli ultimi due, molto meno conosciuti degli altri, per contrapporli alla sorprendente attualità di nozioni matematiche di origine millenaria). Questo sembrerebbe giocare a favore di una delle tesi iniziali, assegnando a ciascuno di loro il merito della “invenzione” di ogni teorema. Ci sono molti che ritengono, invece, rifacendosi ancora oggi alle teorie filosofiche di Platone, che le formule matematiche appartengono ad una sorta di iperuranio, il mondo detto “noumeno” dove le idee matematiche, e non solo matematiche, albergano in attesa di essere scoperte. Questi ultimi sostengono ad esempio che il quadrato costruito sull’ipotenusa sarà uguale, in estensione, alla somma dei quadrati costruiti sui cateti in tutti i triangoli rettangoli, reali o fittizi che siano, e se non l’avesse detto Pitagora qualcun altro prima o poi lo avrebbe “scoperto”. Platone, tra l’altro, riconosceva alla matematica il merito di procedere a partire da determinate ipotesi, da cui scaturivano altre conclusioni che diventavano punto di partenza per altre dimostrazioni, così come doveva svilupparsi ogni conoscenza, proprio perché preesistenti. Anche in Kant Ritroviamo il concetto di “noumeno”, ma in una accezione completamente diversa. Il “Noumeno”, mondo superiore delle idee solo intuibili, in contrapposizione al mondo reale dove siamo inevitabilmente legati alle regole del “Fenomeno”. Kant riteneva che la matematica fosse una pura invenzione della mente, e citava l’esempio dei numeri immaginari, cioè le radici dei numeri negativi, completamente inventati non trovando alcun riscontro nella realtà, anche se oggi la matematica dei numeri negativi è usata in molte applicazioni di tipo pratico. Il fatto che per due punti passasse una sola retta, prendendo un esempio tra i tanti , non era ritenuta una cosa assolutamente valida, ma era solo una conseguenza delle proposizioni matematiche preliminari, comunemente indicati come “assiomi”. (Alcune teorie di geometria non euclidea, sembrerebbero oggi dargli ragione). Riconosceva comunque alla matematica un rigore logico ed un modo di procedere nella conoscenza che lui si augurava potesse essere trasportata nel campo della filosofia. Come potete notare ho citato un altro filosofo greco, Euclide, le cui intuizioni matematiche, create o inventate che siano, sono arrivate intatte fino quasi ai nostri tempi. La geometria non euclidea risale alla prima metà dell’ottocento, ad opera di Georg Friedrich Bernhard Riemann, un matematico tedesco; alla sua opera lo stesso Einstein ha attinto a piene mani per formulare la teoria della relatività generale. Io,
naturalmente, non ho intenzione di sposare nessuna delle due tesi,
anche perché credo che non esista una risposta univoca al quesito,
ma solo solleticare la curiosità di chi legge, sperando di
restituire alla “Matematica” una dimensione e una importanza che non
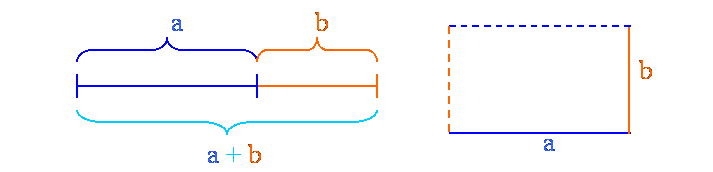
sempre la scuola riesce a fornire. Vediamo di argomentare meglio. I Pitagorici fecero dei numeri un motivo di vita, riconoscendo agli stessi una natura divina. Uno dei loro simboli era il pentacolo, a cui attribuivano un significato di perfezione (Figura 1). Tale figura si ottiene tracciando le diagonali di un pentagono, e formando una stella a cinque punte che ha assunto diversi significati: dal valore demoniaco attribuitogli da certe sette, a simbolo di rivendicazione politica, tornando prepotentemente in auge di recente con il libro “Il codice Da Vinci”. Una delle caratteristiche, forse ignote, di tale figura è che la diagonale ed il lato del pentagono sono in rapporto aureo tra di loro. La “sezione aurea”, o sezione divina di Fidia, particolarmente cara al frate e matematico Luca Pacioli (1445-1517) che teorizzò l’uso della “divina proporzione” in ogni campo artistico, è riportata nella figura seguente. Prendendo un segmento e dividendolo in due parti, si ha che queste parti sono in rapporto aureo fra loro se tutto il segmento è in rapporto alla porzione maggiore, allo stesso modo della porzione maggiore rispetto alla minore. In formule (a+b) : a = a : b .
Questo rapporto ha il valore qui riportato, Questo numero ha diverse particolarità matematiche e ci sono diversi modi per ottenerlo, riportati sotto; metodi ripetitivi o funzioni particolari, il risultato è sempre lo stesso. Se facciamo il suo inverso 1/f , troviamo il numero 0,61803398871989484.. cioè f – 1. Non è sorprendente ? La sezione aurea e in particolare il rettangolo aureo, costituito da lati che sono in rapporto aureo fra loro (a destra nella figura sopra), è stato utilizzato nei più svariati campi dove il senso estetico e l’armonia delle parti dovessero, non solo nell’antichità, essere in particolare equilibrio. Nelle figure che seguono si vede il Partenone (figura 2), costruito tutto su proporzioni auree, e un arco (figura 3), così come lo concepivano nel Rinascimento, durante il quale l’uso della sezione aurea era molto diffuso.
Figura 2 Figura 3 In tempi più moderni lo hanno utilizzato moltissimi architetti, in particolare Le Corbusier, del quale viene riportato, figura 4, il celeberrimo “modulor”, dove sono riportate le varie proporzioni del corpo umano per la costruzione su base ergonomica di sedie, scale e quant’altro. Figura 4 Figura 5 La figura 5 mostra l’utilizzo della sezione aurea per la realizzazione della scultura “Dorifor” dello scultore greco Policleto. L’idea è la stessa e sono passati millenni. Per non parlare della pittura, di ogni epoca, dove non mancano certo applicazioni della proporzione divina. Il tutto per creare una struttura armonica all’interno del quadro, e garantire una sicura riuscita dello stesso. Per qualche motivo ignoto sembra che la psiche umana gradisca in modo particolare strutture che rispondono a questi criteri, come possiamo osservare nei quadri riportati di seguito.
Figura 6 Figura 7 La cosa sorprendente, e non ho voluto di proposito mostrare le applicazioni della sezione aurea a quadri che appartengono alla classicità di ogni tempo, da Leonardo a Botticelli a Piero della Francesca e altri, è che questi esempi sono di arte recentissima, se non contemporanea. Il quadro in figura 6 è l’opera “La parade du cirq” del pittore divisionista francese Georges Seurat, mentre la figura 7 mostra un’opera dell’inconfondibile Mondrian. In quasi tutti i quadri di quest’ultimo troviamo una serie di rettangoli aurei. Per chiudere su questo argomento mi piace citare un pittore alquanto controverso e altrettanto geniale, tra i fondatori del surrealismo: Salvador Dalì. Nelle due opere che seguono ha utilizzato sicuramente la sezione aurea. Nel quadro “Il Sacramento dell’ultima cena” di figura 8, infatti, le dimensioni sono quelle auree e ci sono diversi elementi che la richiamano (qualche cenno all’uomo vitruviano di Leonardo e vari pentagoni. Per la realizzazione del secondo ( figura 9), la “Leda atomica”, l’artista si è avvalso della collaborazione di un matematico rumeno, proprio per costruire le proporzioni adeguate fra i vari elementi, infatti quella che sembra una “A” sospesa, è un compasso.
Figura 8 Figura 9 C’è chi ha analizzato le composizioni musicali di diversi artisti, trovando anche in esse qualcosa legata alla sezione aurea. La struttura di molte sinfonie e concerti, in particolare di Debussy e di Bartok, per non parlare di composizioni più moderne di musica elettronica, tipo quella dell’autore greco Xenakis, sembra rispondere ad una successione matematica ben precisa. Qui forse è il caso di allargare un po’ il discorso per far capire meglio come stanno le cose. Leonardo da Pisa (1170-1250), comunemente noto come Leonardo Fibonacci è universalmente conosciuto per una serie numerica, chiamata appunto di Fibonacci, che viene riportata di seguito: 1 1 2 3 5 8 13 21 34 55 89 144 233 377 ….. Qual è la sua particolarità? A prima vista sembra una serie di numeri senza particolare significato. Ad un'attenta lettura si scopre che ogni termine della successione è ottenuto sommando i due termini precedenti. Se però facciamo il rapporto fra un numero ed il precedente, man mano che il numero cresce, il risultato del rapporto si avvicina sempre più al valore del rapporto determinato per la sezione aurea. 89/55 = 1,61818181…. 233/144 = 1,6180555…. 377/233 = 1,618025.. Assolutamente sorprendente, tanto che oramai non si fa più distinzione fra sezione aurea e numeri di Fibonacci attribuendo ad essi lo stesso significato, quasi magico o divino. Quando si dice che la sezione aurea è stata utilizzata nella musica, quello che si intende è che nella struttura temporale delle opere, o nelle battute, si è seguita in qualche modo la serie di Fibonacci. In molti casi, specialmente in certa musica elettronica e sperimentale, come citato prima, sono le note stesse, che, come ricordo corrispondono a determinate frequenze, sono costruite in modo che il loro rapporto sia uguale al numero che abbiamo indicato con f, oramai a noi familiare. Tanto per completezza, c’è chi ha trovato la serie di Fibonacci anche in alcune opere letterarie ed in poesia. Mi piace qui riportare una poesia di Puskin che sembra costruita con questo criterio, “Il ciabattino”. Una volta un ciabattino guardava un quadro e indicava un errore nella calzatura prendendo subito un pennello il pittore correggeva. Ecco, con orgoglio, il ciabattino continuava: “La faccia mi pare un po’ sformata e questo petto non è un po’ troppo nudo?” All’improvviso Apollo con impazienza lo interrompe “Il tuo giudizio, amico, non vale più di una scarpa!” Ho un amico, per esempio non so quali argomenti conosce benché sia esperto a parole. Ma che il diavolo se lo porti a parole. Ma che provi a giudicare i suoi stivali. Se proviamo a contare i versi ne troviamo 13 in totale, 8 nella prima parte e 5 nella seconda. Tre numeri della serie di Fibonacci, messi alla rovescia. Qualcuno a questo punto potrebbe chiedersi se tutto quello che ho detto ha un nesso con la questione iniziale sulla matematica. In fondo si tratta di libere scelte dei vari artisti, che hanno semplicemente utilizzato una relazione matematica riconoscendogli un qualche merito. Ancora un attimo di pazienza. Se prendiamo un rettangolo aureo e ne ricaviamo un quadrato, la parte rimanente è ancora un rettangolo aureo, e possiamo ripetere la stessa operazione su ogni rettangolo ottenuto, sempre più piccolo. Se tracciamo un arco di cerchio su ogni quadrato, come mostrato in figura 10, otteniamo una forma a spirale che è la spirale logaritmica. In natura abbiamo molti esempi di “oggetti” costruiti con questa figura, come evidenzia la figura 11, una comune conchiglia. La stessa struttura la possiamo trovare all’interno del nostro orecchio, nella parte chiamata “coclea”.
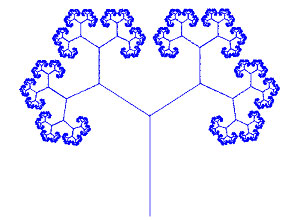
Figura 10 Figura 11 In natura ritroviamo molti esempi di applicazione della sezione aurea: nei girasoli, nell’ananas, nelle pigne, nei fiori e nel modo di distribuzione delle foglie in alcune piante, che sembrano seguire la successione di Fibonacci. Una curiosità: questa serie non è nata da studi matematici, ma dallo studio della riproduzione dei conigli: il numero di esemplari, secondo lo stesso studioso, generazione dopo generazione, riproduce esattamente la successione scritta. Questo confermerebbe che la natura predilige la sezione aurea, e quindi la matematica ha semplicemente scoperto una legge interna della natura stessa. Si potrebbe giustificare l’utilizzo della sezione aurea nella musica dicendo che, l’orecchio percepisce come armonici i suoni costruiti in modo tale da rispettare la sua stessa struttura, ma si potrebbe anche affermare che è l’orecchio che si è adattato alla natura che rispetta la “divina proporzione”. Qualche studioso, in particolare lo psicologo Gustav Theodor Fechner (1801-1887), studiò la reazione degli uomini alla sezione aurea arrivando a sostenere che la mente umana possiede un meccanismo che genera sensazioni piacevoli di fronte al rapporto aureo; e c’è chi ha scritto che quando sediamo su una panchina vuota, non scegliamo né il bordo né il centro, ma inconsciamente occupiamo una posizione tale da dividere la panchina in proporzioni auree. Mi sembra veramente eccessivo. Ma continuiamo il discorso. Se prendiamo un segmento e all’estremità dello stesso aggiungiamo due segmenti in rapporto aureo con quello di partenza e se ripetiamo questa operazione sugli altri due e così via, otteniamo la figura 12, un albero aureo. Questa figura assomiglia a quella serie di disegni curiosi e a volte misteriosi che vanno sotto il nome di “Frattali”. I frattali, scoperti da Benoit Mandelbrot nel 1975, sono figure geometriche caratterizzate dal ripetersi sino all'infinito di uno stesso motivo su scala sempre più ridotta. Se operiamo un ingrandimento troviamo sempre una struttura simile al tutto. Essi sono generati da un'operazione iterativa, cioè ripetitiva all’infinito, sulle proprie parti. Sembra che tutto in natura sia frattale (figura 13, 14, 15,16).
Figura 12 Figura 13
Figura 14 (la felce) Figura 15 (foglia di platano) Figura 16 (albero)
I frattali sono in grado di descrivere il modo in cui foglie e piante si sviluppano e crescono, il modo in cui si apre il delta di un fiume, o come si frastagliano le coste, come si sviluppa un organismo, il sistema nervoso, i bronchi, e potrei continuare un lunghissimo elenco. Nelle figure che seguono, per esempio (figure 17 e 18) , è illustrato come funzionano i frattali nella costruzione di un fiocco di neve.
Figura 17 Figura 18 Anche in letteratura non mancano esempi di applicazione dei frattali. Ne vorrei citare in particolare due. Jorge Luis Borges, geniale scrittore argentino,in particolare nel racconto: “La biblioteca di Babele”, una biblioteca simbolo dell’universo dove le sale si succedono all’infinito e dove ci sono tutti i libri possibili, tutti quelli scritti e da scrivere con tutte le possibili combinazioni delle lettere dell’alfabeto, una Babele, insomma. E nel racconto “Il giardino dei sentieri che si biforcano”, che è proprio l’immagine letteraria dell’albero frattale descritto sopra. L’altro autore è Italo Calvino: nei racconti di “Palomar” adotta proprio una tecnica frattale strutturando il libro in tre racconti, ognuno dei quali è diviso in tre capitoli suddivisi in tre parti ciascuno. In ogni racconto, poi, si parla di esperienze di tre tipi: visivo, culturale e speculativo. Egli stesso afferma : “..volevo parlarvi della mia predilezione per le forme geometriche, per le simmetrie, per le serie, per la combinatoria, per le proporzioni numeriche, spiegare le cose che ho scritto in chiave della mia fedeltà all’idea di limite, di misura …”. In campo artistico osservate l’uso fatto da Escher di strutture ricorrenti di tipo frattale (Figura 19). E non si può non citare Johan Sebastian Bach che nelle sue composizioni utilizza le strutture ricorrenti e ripetitive tutte uguali a se stesse in un moto che può continuare all’infinito, tipiche dei “Canoni” musicali , e delle “fughe” ben note. Anche il cinema non è esente dalle strutture frattali. Nel film “Smoking/No smoking” di Alain Resnais la storia, o meglio i diversi possibili sviluppi di una storia a seconda delle scelte dei protagonisti, si dipanano e si dividono in vari filoni. Il semplice fatto di accendere o meno una sigaretta determina due serie diverse di conseguenze, aprendosi in due diversi film, da cui il titolo. Poi, ciascun film prende in esame un'ulteriore serie di diramazioni dei singoli destini andando a vedere che cosa accadrà o sarebbe potuto accadere dopo. Ciascun film alla fine avrà proposto sedici storie e possibili conclusioni diverse. Non è la struttura dell’albero frattale di cui abbiamo parlato prima? Figura 19 Ebbene i frattali sono oggetti matematici esprimibili in formule, secondo leggi di iteratività e “affinità” in senso geometrico, come traslazioni, rotazioni, similitudini fra forme. Tutto sembrerebbe confermare la teoria di Galileo che affermava :” "…Io veramente stimo il libro della filosofia esser quello che perpetuamente ci sta aperto innanzi a gli occhi ; ma perchè é scritto in caratteri diversi da quelli del nostro alfabeto , non può esser da tutti letto : e sono i caratteri di tal libro triangoli , quadrati , cerchi , sfere , coni , piramidi ed altre figure matematiche , attissime per tal lettura…". La matematica è il linguaggio in cui è scritta la natura, e per capirla bisogna usare metodi matematici, coerenti, logici e rigorosi. Nasce con Galilei, infatti, la fisica sperimentale. Allora la matematica è una scoperta, si potrebbe concludere, ma le cose non stanno proprio così. Proprio il frattale
di Mandelbrot (figura 20) nacque durante lo studio di una funzione
costruita con numeri complessi. Il matematico che riconobbe per
primo la necessità di ampliare i numeri fino ad allora conosciuti
con altri a + j b
dove
j =
numeri senza senso per la realtà. Molti matematici, dopo Bombelli si sono interessati dei numeri complessi, in particolare lo svizzero Argand (1768-1822) e il tedesco Carl Friederich Gauss (1777-1855), ai quali si deve il metodo per rappresentare i numeri complessi, scegliendo un sistema di assi cartesiani e riportando sull’asse orizzontale le parti reali di numeri complessi e su quello verticale le parti immaginarie che prende il Figura 20 nome di piano di Argand-Gauss. Questo metodo è stato usato da Mandelbrot per la rappresentazione del suo frattale e viene utilizzato in diversi campi, dall’elettrotecnica alla fisica, ogni volta che se ne presenta la necessità. La stessa fisica quantistica è stata formulata in termini di grandezze complesse, le funzioni d’onda, senza le quali tale teoria non avrebbe potuto essere formalizzata. Questo sembra un ulteriore conferma dell’ordine matematico della natura. Eppure i numeri complessi sono stati in qualche modo inventati. L’altro
problema della matematica a cui ci riconducono i frattali è il
concetto di infinito. Questo concetto era nettamente rifiutato dai
filosofi antichi. Vi sarà senz’altro capitato di incontrare il
paradosso di Achille e la Tartaruga,
forse il più famoso tra i paradossi matematici: noi lo prenderemo
come punto di partenza per esplorare il modo in cui il concetto di
infinito fosse particolarmente indigesto al mondo greco classico,
caratterizzato da un “Horror infiniti”
che portò a cercare di eliminare il più possibile l'uso di questo
concetto all'interno del discorso matematico.
Figura 21 Qual è la soluzione? Ci sono voluti duemila anni per scoprire che la somma di infiniti termini non dà necessariamente come risultato un numero infinitamente grande, ma può dare come risultato un numero finito. La scoperta delle serie numeriche, e il paradosso di Achille e la tartaruga è risolvibile proprio in termini di una di esse, ha portato alla definizione di convergenza o divergenza, a seconda che la somma di infiniti termini dia un valore finito o infinito. Questo sembra un concetto difficile da digerire, ma oramai l’analisi numerica è data per acquisita. Ricordate il frattale che da origine al fiocco di neve di figura 17?. Questa figura evidenzia un’altra particolarità dei frattali. Se osserviamo infatti le prime tre figure notiamo che ad ogni passaggio la misura di un lato diventa 4/3 del lato che avevamo nel passaggio precedente, per cui la misura del perimetro della figura diventa 4/3 del perimetro precedente. Questo da origine ad una serie matematica di tipo divergente, pn = (4/3)(n-1)*p dove p rappresenta il perimetro del triangolo di partenza e n il numero di iterazioni operate nella costruzione della figura, cioè il perimetro di tale figura è infinito, mentre la sua area complessiva ha un valore finito essendo possibile racchiuderla in una circonferenza di un opportuno raggio definito. Questo ci riconduce a Shakespeare che al suo Amleto fa dire: «Oh Dio, potrei essere rinchiuso in un guscio di noce e sentirmi re dello spazio infinito». Tra i tanti che hanno cercato l’infinito in un guscio di noce vorrei citare Stephen Hawking, il fisico teorizzatore dei “buchi neri” che ha intitolato una sua opera di divulgazione proprio “L’universo in un guscio di noce”, intendendo che lo spazio entri il quale si sarebbe originato il “Big bang”, da cui avrebbe origine tutto il nostro universo, non era più grande di un guscio di noce . L’infinito in uno spazio limitato è un’idea molto affascinante. Bisognerebbe precisare che si parla di “tendenza ad infinito”, e non di “valore infinito”. Gli studi di Georg Cantor (1845-1918), anzi, hanno portato alla scoperta di infiniti di ordine superiore, a quelli che lo stesso definì “transfiniti”. Cantor introduce il criterio della numerabilità, intendendo per numerabile qualunque sequenza che possa essere messa in corrispondenza biunivoca, uno a uno per intenderci, con i numeri naturali che sono infiniti, nel senso che qualunque numero prenda se ne trova sempre uno più grande. Giacomo Leopardi nello Zibaldone così scriveva:«Il credere l'universo infinito è un'illusione ottica: almeno tale è il mio parere. Come si è trovato per esperienza che il globo terracqueo il quale pare infinito, ha pure i suoi limiti, così, secondo analogia, si deve credere che la mole intera dell'universo, il quale ci pare infinito per la stessa causa... I primitivi credevano ancora e credono che le stelle che noi veggiamo non si potessero contare, cioè fossero infinite di numero... Niente infatti nella natura annunzia l'infinito, l'esistenza di alcuna cosa infinita. L'infinito è un parto della nostra immaginazione». Aristotele affermava: «In verità capita che l'infinito sia proprio il contrario di quel che si dice. Difatti, l'infinito non è ciò al di fuori di cui non c'è nulla, ma ciò al di fuori di cui c'è sempre qualcosa». E ancora Aristotele a proposito dei numeri: «E' conforme a ragione che nella serie numerica il più piccolo sia il termine, ma che procedendo verso un numero maggiore, ogni quantità venga superata... procedendo verso il più grande, non c'è grandezza infinita. E la ragione è che l'unità numerica è indivisibile mentre il numero è una pluralità di unità...Sicché il numero è infinito in potenza, ma non in atto». E’ proprio questo il problema. L’idea dell’infinito è applicabile alla matematica che gestisce i concetti, ma non alla realtà. Bernard Bolzano (1781-1848), sacerdote cattolico nato a Praga da famiglia di origine italiana, grande matematico, sosteneva: «Che l'infinito sia contrapposto ad ogni mero finito è già espresso nel termine stesso. I matematici hanno fatto uso del termine infinito in altro senso che questo: se trovano una quantità maggiore di qualsiasi numero di unità assunte, la chiamano infinitamente grande; se trovano una quantità così piccola che ogni suo multiplo è minore dell'unità, la chiamano infinitamente piccola; né riconoscono alcuna altra specie di infinito oltre queste due e oltre specie da esse derivate, infinitamente più grandi o infinitamente più piccole, che discendono tutte dallo stesso concetto. Alcuni filosofi però, per esempio Hegel e i suoi seguaci, non sono soddisfatti di questo infinito dei matematici e lo chiamano con disprezzo cattiva infinità, rivendicando la conoscenza di un infinito molto superiore, il vero infinito, l'infinito qualitativo, che essi trovano solo in Dio, e in generale nell'Assoluto». Sempre Borges, in uno dei suoi racconti, parla di un libro fatto di infinite pagine infinitamente sottili, eppure un libro di dimensioni simili a quella di qualunque altro. La particolarità di questo libro è che aprendolo a caso non potrò mai trovare la stessa pagina e sarà sempre nuovo, nel senso dei contenuti. Questa l’idea letteraria. E’ evidente che si tratta di una invenzione dello scrittore, ma matematicamente esso è una cosa fattibile, in principio. E’ esattamente l’operazione che si fa in analisi matematica, ad esempio con l’operazione di integrale definito, sommando infiniti termini di valore infinitamente piccolo e ottenendo un valore finito, l’area di una figura o il volume di un solido. La conclusione allora potrebbe essere che la matematica è una invenzione? Steven Weinberg, uno dei fisici moderni più quotati, premio nobel per la fisica, così affermava in una conferenza: “Se la matematica sia un’invenzione o un codice naturale che dobbiamo ancora capire, non lo sappiamo, ma noi ci affidiamo ai numeri per previsioni, probabilità, scala, simmetria. Man mano che cresce, il mondo matematico rivela nuovi territori inesplorati in cui noi ci muoviamo con istinto e autorità, con immaginazione e incertezza”. Resta il mistero di come la matematica, scoperta o inventata che sia, riesca a descrivere in formule matematiche la realtà fisica che ci circonda. Roger Penrose, altro fisico matematico vivente di assoluto rilievo, così la pensa a proposito: “La matematica è una idealizzazione. Qui non parliamo di segni tracciati nella sabbia, parliamo di determinate strutture ideali che richiamano un certo mondo: sono strutture idealizzate che ci ricordano la realtà”.
Domenico Di Bucchianico
|
|||






















 numeri, fu Rafael Bombelli (1526-1573), matematico bolognese. Nel
trovare le soluzioni delle equazioni algebriche ci si imbatte spesso
in radici di numeri negativi, che determinano soluzioni del tipo
numeri, fu Rafael Bombelli (1526-1573), matematico bolognese. Nel
trovare le soluzioni delle equazioni algebriche ci si imbatte spesso
in radici di numeri negativi, che determinano soluzioni del tipo 