I  filtri  sono  dispositivi in grado di presentare o meno in uscita  il corrispondente  segnale di ingresso, in relazione alla frequenza dello stesso. Possono classificarsi, in base alla rapidità di risposta, in filtri del primo,secondo,  terzo ordine ..... I circuiti  che andremo ad  analizzare sono quelli di primo  ordine; essi hanno una rapidità di risposta piuttosto bassa e la funzione di trasferimento presenta soltanto un polo.
 
 

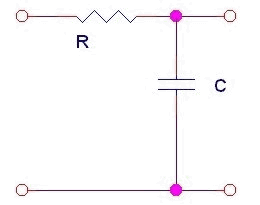
Questi dispositivi hanno una funzione di transferimento pari a:

Confrontandola con la struttura della funzione di trasferimento del generico sistema lineare e tempo invariante:

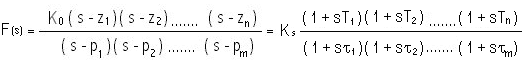
Si ha F(s):

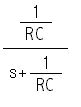
da cui p = - 1/RC e t= RC.
La funzione di transferimento non possiede zeri, ma solo un polo a parte reale positiva,il modulo si mantiene costante fino a valori della pulsazione prossimi ad infinito.

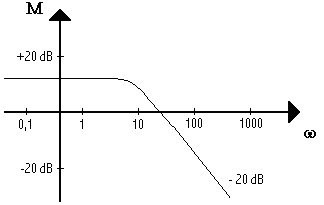
La fase è prossima allo 0 per le basse frequenze e tende a -90° per le alte frequenze. Il campo di commutazione ( periodo nel quale avviene il passaggio dal 10 al 90 per cento della fase del segnale ) si trova in prossimità della frequenza di taglio, corrispondente al polo della funzione F(s).

Il sistema in esame è di tipo zero ed è stabile ad anello aperto perchè la sua funzione di trasferimento  non presenta  poli a parte reale positiva. Per verificare la stabilità del sistema ad anello chiuso possiamo ricorrere anche al criterio di Nyquist. Ponendo s = jw si ha:

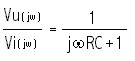
Per w = 0    risulta   | F ( jw) | = 1
                            f = - arctg wCR/1 = 0°

Per si ottiene | F ( jw) | = 0
                                     f = - arctg wCR/1 = - 90°

Il diagramma polare ha origine nel punto di coordinate ( 1,j0 ) del semiasse positivo e la fase della funzione è negativa per  w>0. Pertanto il vettore rappresentativo della F ( jw) ruota in verso orario e il diagramma di Nyquist risulta tangente nell'origine al semiasse immaginario negativo visto che per w= avremo f = - 90°.

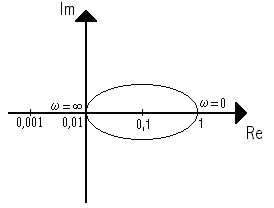
Il diagramma di Nyquist mostra che il vettore rappresentativo della F ( jw) non compie alcuna rotazione attorno al punto critico ( -1,j0 ) per w che varia da -  a .  Per il criterio ristretto di Nyquist il sistema risulta stabile ad anello chiuso.

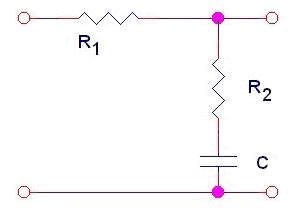
Questi dispositivi hanno una funzione di transferimento pari a:

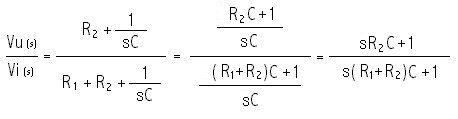
Si ha F(s):

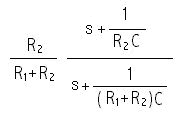
da cui p = -1/( R1 + R2 )C  e z = -1/R2C ; T = R2C, t= (R1 + R2 )C
La funzione di transferimento possiede uno zero ed un polo entrambi aparte reale positiva. L'andamento del modulo è costante fino al polo, tende a 0 per frequenze superiori e torna ad essere costante per frequenze molto superiori allo 0 da questo punto il sistema sarà caratterizzato da un guadagno costante con valore dipendente dalle resistenze R1 ed R2.

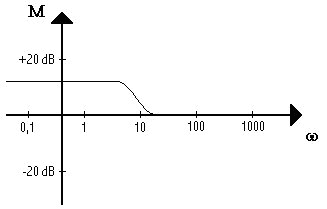
La fase è prossima allo 0 per le basse frequenze e tende a - 90° dopo aver incontrato il polo; tornerà nuovamente a 0 dopo aver incontrato anche lo zero. Il periodo nel quale la fase di uscita si discosta da quella di ingresso sarà dato dalle resistenze R1 ed R2.

Il sistema in esame è di tipo zero ed è stabile ad anello aperto perchè la sua funzione di trasferimento  non presenta poli a parte reale positiva. Per verificare la stabilità del sistema ad anello chiuso possiamo ricorrere anche al criterio di Nyquist. Ponendo s = jw si ha:

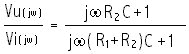
Per w = 0      risulta   | F ( jw) | = 1
                                f = arctg wR2C/1- arctg w( R1 + R2 )C/1 = 0°

Per si ottiene  | F ( jw) | = 0
                                          f = arctg wR2C/1- arctg w( R1 + R2 )C/1 = 0°

Il diagramma polare ha origine nel punto di coordinate ( 1,j0 ) del semiasse positivo e la fase della funzione è negativa per  w>0. Pertanto il vettore rappresentativo della F (  jw )ruota in verso orario
ed il diagramma descritto,si rappresenta interamente nel quarto quadrante.

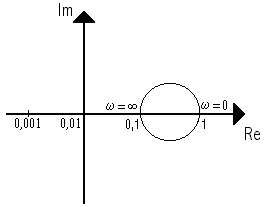
Il diagramma di Nyquist mostra che il vettore rappresentativo della F ( jw ) non compie alcuna rotazione attorno al punto critico ( -1,j0 ) per w varia da -  a . Per il criterio ristretto di Nyquist il sistema risulta stabile ad anello chiuso.